Luiz Antônio Moro Palazzo
Universidade Católica de Pelotas
Escola de Informática
lpalazzo@atlas.ucpel.tche.br
____________________________________________________________________________
Este artigo introduz um conjunto de conceitos provenientes de estudos teóricos e empíricos na ciência do caos e da complexidade com ampla aplicação na modelagem de sistemas computacionais adaptativos, evolutivos de simulação e de otimização em geral. Tais sistemas são aqui considerados sob o ponto de vista de sua organização e dos fenômenos que a provocam e sustentam. Os conceitos de auto-organização, sistemas complexos adaptativos, criticalidade, fronteira do caos e evolução são comentados, destacando-se o modo como estão relacionados na formação de um padrão estrutural coerente observado freqüentemente na natureza. Aborda-se também o emprego desses conceitos na modelagem de sistemas computacionais e suas perspectivas de aplicação como um paradigma para a construção de sistemas complexos de informação.
_______________________________________________________________
O estudo de sistemas complexos cresceu muito nos últimos anos, não obstante ser o próprio conceito de complexidade definido muito vagamente e segundo diversas teorias alternativas [KOL65] [CHA75] [CRU94]. O termo “complexidade” vem do latim, complexus, que significa entrelaçado ou torcido junto. Isto pode ser interpretado da seguinte maneira: para se ter um sistema complexo é necessário (1) duas ou mais diferentes partes ou componentes e (2) estes componentes devem estar de algum modo interligados formando uma estrutura estável [HEY88]. Aqui se encontra a dualidade básica entre partes que são ao mesmo tempo distintas e interconectadas. Um sistema complexo não pode então ser analisado ou separado em um conjunto de elementos independentes sem ser destruído. Em conseqüência não é possível empregar métodos reducionistas para a sua interpretação ou entendimento. Se um determinado domínio é complexo ele será, por definição, resistente à análise.
A consciência da existência de fenômenos que não podem ser reduzidos às suas partes em separado conduziu ao holismo, que pode ser visto como uma corrente de pensamento oposta ao reducionismo. O holismo propõe a observação de um fenômeno complexo como um todo, ao invés de como uma coleção de partes. Esta visão, entretanto, também negligencia um importante aspecto das entidades complexas: o fato de que elas são compostas de partes distintas, mesmo que essas partes se encontrem em estreito relacionamento.
Considerar um fenômeno como um todo porém significa identificá-lo com uma unidade, isto é, fundamentalmente simples. Na construção de uma ciência da complexidade deve-se portanto buscar uma visão capaz de transcender a polarização entre holismo e reducionismo, permitindo a modelagem de sistemas que apresentam simultaneamente a característica da distinção (sendo portanto separáveis do todo em uma forma abstrata) e da conexão (sendo portanto indissociáveis do todo sem a perda de parte do significado original).
Uma forma simples de modelo que satisfaz simultaneamente esses dois requisitos aparentemente contraditórios é o conceito matemático de rede. Uma rede consiste de nodos e de conexões ou arcos entre os nodos. Estes podem ser vistos como partes de um sistema complexo, enquanto que as conexões irão corresponder às relações que estabelecem entre si. Esta visão tem a propriedade de ser reversível, isto é, pode-se também ver os nodos como conexões entre os arcos, que então são tomados como os elementos componentes.
Assim a abordagem reducionista pode ser pensada simplesmente como um método que tenta eliminar tanto quanto possível as conexões, enfatizando a individualidade dos nodos, enquanto que a abordagem holística elimina tanto quanto possível as distinções entre os nodos. Neste sentido, ambos os métodos “reduzem” um fenômeno complexo a uma representação basicamente mais simples (um conjunto solto de nodos diferenciados ou uma massa de conexões entre nodos iguais), negligenciando uma parte essencial das características do fenômeno.
O termo complexidade é por vezes também tomado como um sinônimo de desordem ou caos. Entretanto, somente a noção de desordem não é suficiente para definir complexidade. É necessário também entender o conceito de ordem. Exemplos simples de ordem são estruturas simétricas (p.ex: reticulados cristalinos). A simetria é definida matematicamente como a invariância sob um conjunto de operações ou transformações (não necessariamente um grupo). A principal característica de um sistema ordenado é a sua previsibilidade (espacial ou temporal). Não é necessário conhecer o sistema como um todo para reconstruí-lo ou prever sua estrutura: o sistema é redundante.
Levada ao limite esta definição, na tentativa de produzir um sistema em ordenação máxima, obtém-se um sistema caracterizado pelo fato de ser invariável sob qualquer possível transformação. A única estrutura possível para tal sistema se caracteriza por total homogeneidade: deve ser possível mapear o sistema de uma parte qualquer para outra sem que nenhuma modificação ocorra. Além disso o sistema deve possuir uma extensão infinita, porque de outro modo se poderia imaginar transformações que mapeassem de uma parte do sistema para algum elemento fora de seus limites. Em outras palavras, um sistema de ordenação máxima iria corresponder a um vácuo clássico, isto é, a uma substância estendida ao infinito na qual nenhuma parte, componente ou estrutura interna pode ser distinguida. Tal sistema é claramente o oposto do que se tomou como um sistema complexo, que se caracteriza justamente por possuir uma estrutura interna diferenciada.
A desordem, por outro lado, é caracterizada pela ausência de invariância, isto é, pela ausência de transformações (não triviais) que não teriam qualquer efeito distinguível sobre o sistema. No limite isto significa que qualquer parte do sistema, por insignificante que seja, deve ser diferente ou independente de qualquer outra parte. Um exemplo aproximado de tal sistema seria um gás perfeito: em geral a velocidade de duas moléculas diferentes seriam distintas e independentes, não havendo qualquer coordenação sobre as diferentes moléculas. Observado mais de perto entretanto o fenômeno de um gás perfeito apresenta diversas invariâncias: o movimento de uma molécula de gás é contínuo durante o curto intervalo de tempo em que ela não colide com outras moléculas, caracterizado pela conservação de momento. Além disso o espaço entre as moléculas pode ser visto com um vácuo clássico, que como se viu é ordenado.
Em um sistema de máxima desordem deve-se ter partículas com qualquer momento físico aparecendo e desaparecendo em qualquer instante no tempo e qualquer posição no espaço. Um exemplo de tal sistema é o vácuo como é visto pela teoria quântica. As flutuações quânticas do vácuo continuamente criam e destroem partículas virtuais, assim denominadas porque são tão instáveis que em princípio são impossíveis de observar. Na prática isto significa que o vácuo quântico não pode ser distinguido do vácuo clássico. Isso conduz à conclusão de que tanto a perfeita ordem quanto a perfeita desordem no limite correspondem ao vazio, isto é, à ausência de qualquer forma de complexidade.
O passo seguinte no estudo da complexidade corresponde à análise de como um sistema complexo evolui, isto é, como ele se modifica ao longo do tempo. A invariância limitada postulada na seção anterior não se aplica somente a transformações geométricas ou espaciais, mas também a transformações temporais ou dinâmicas. Isto significa que certas partes ou estruturas do sistema serão conservadas durante uma certa evolução de tempo enquanto que outras irão se modificar. Até aqui esta descrição parece bastante trivial: uma parte do sistema se modifica enquanto que outra permanece sem modificações. É necessário entretanto algum método para identificar quais os subsistemas que irão mudar e quais os que irão permanecer inalterados.
A evolução de sistemas complexos, de acordo com esta visão, é caracterizada por um intrincado emaranhado de ordem ou invariância e desordem ou variação. Suponha-se que haja uma subestrutura relativamente invariante (isto é, não afetada por um certo conjunto de transformações) em um sistema complexo. Isto significa que enquanto os processos internos do sistema pertencerem a esta categoria de transformação a subestrutura irá permanecer invariável. Na evolução biológica o agente de seleção é o ambiente, que demanda uma certa forma de adaptação do sistema, que de outro modo não irá sobreviver. No estudo da complexidade entretanto, sem fazer uma distinção a priori entre um sistema e seu ambiente externo não é possível empregar tal critério. A distinção entre o sistema que tenta sobreviver e seu ambiente, que pode permitir ou dificultar esta sobrevivência, é por si só uma característica dos sistemas complexos em geral. Discorrer sobre a sobrevivência de um subsistema em um todo maior implica em que se deve ter alguma maneira de reconhecer tais subsistemas invariantes inseridos em ambientes em evolução. Em outras palavras os subsistemas estáveis devem ser distinguidos como indivíduos. A dinâmica de variação-restrição é o princípio sobre o qual se baseia a invariância relativa das distinções em sistemas complexos.
O princípio da variação e retenção seletiva [HEY88] foi elaborado a partir deste ponto de vista. Por definição um sistema complexo consiste em um certo número de subestruturas distintas submetidas à variação. Como a variação não é absoluta ou completa, essas subestruturas deverão apresentar alguma invariância ou estabilidade. Isto significa que as subestruturas não irão mudar todas ao mesmo tempo. Há alguma forma de inércia ou continuidade que limita a mudança. Isto permite considerar uma subestrutura como possuindo uma identidade estável durante um certo (talvez infinitesimal) espaço de tempo. O que pode então mudar durante este intervalo? Tanto as relações ou conexões entre a subestrutura considerada e as demais quanto a organização interna das partes da subestrutura mudam. O primeiro processo pode ser denominado (re)combinação e o segundo mutação.
Outra questão fundamental é: “De onde vem a ordem?” Segundo as leis gerais da termodinâmica parece que os processos dinâmicos tendem a seguir os caminhos de menor consumo de energia até que o sistema encontre um ponto de equilíbrio onde permanecerá enquanto não sofrer perturbação. Há diversos exemplos na natureza de sistemas e organismos que apresentam elevada energia e organização internas em aparente desafio às leis da física. Alguns deles são:
Partículas de limalha de ferro que se alinham segundo as linhas de força do campo magnético a que são submetidas;
Partículas d’água que suspensas no ar formam nuvens;
Formigas ou abelhas que crescem a partir de um zigoto até formar um complexo sistema de células que então por sua vez participa de uma sociedade altamente estruturada e hierarquizada.
A organização surge espontaneamente a partir da desordem e não parece ser dirigida por leis físicas conhecidas. De alguma forma a ordem surge das múltiplas interações entre as unidades componentes e as leis que podem governar este comportamento não são bem conhecidas. A perspectiva comportamental de um sistema auto-organizável poderia revelar como padrões espaciais e temporais - tais como caminhos, limites, ciclos e sucessões - poderiam surgir em comunidades heterogêneas complexas. O entendimento dos mecanismos de auto-organização pode conduzir à construção de modelos mais informativos e precisos. Os primeiros modelos de formação de padrões utilizados baseavam-se em uma abordagem top-down onde os parâmetros descreviam os níveis mais altos dos sistemas. Segundo este enfoque a dinâmica das populações é representada também em seus níveis mais elevados e não como resultado da atividade que ocorre ao nível mais baixo dos indivíduos.
A abordagem top-down viola dois princípios básicos dos fenômenos populacionais, que são individualidade e localidade [KAW94]. A individualidade tenta levar em conta as diferenças entre os indivíduos. Tais diferenças, ainda que muito pequenas, podem conduzir a resultados radicalmente diferentes na evolução das populações ao longo do tempo. Por localidade pretende-se significar que cada evento possui uma localização e um escopo de influência. Ignorar a localidade dos eventos obscurece fatores que poderiam contribuir para uma visão mais clara da dinâmica espaço-temporal dos sistemas.
É necessário a um sistema satisfazer diversas pré-condições e valer-se de vários mecanismos para promover a auto-organização [NIC89] [FOR94]. Tais mecanismos são de certa forma redundantes e pouco definidos, entretanto permitem avaliar intuitivamente o potencial de auto-organização dos sistemas. São eles:
Abertura Termodinâmica: Em primeiro lugar o sistema (uma unidade reconhecível, tal como um órgão, um organismo ou uma população) deve trocar energia e/ou massa com o seu ambiente. Em outras palavras, deve haver um fluxo não-nulo de energia através do sistema.
Comportamento Dinâmico: Se um sistema não está em equilíbrio termodinâmico, a única opção que resta para o seu comportamento é assumir algum tipo de dinâmica, significando que o sistema encontra-se em contínua mudança.
Interação Local: Uma vez que todos os sistemas naturais apresentam inerentemente interações locais, esta condição parece ser um importante mecanismo para a auto-organização e como tal deve ser incorporada aos modelos que a representam.
Dinâmica Não-Linear: Um sistema com laços de feedback positivo e negativo é modelado com equações não-lineares. A auto-organização pode ocorrer quando existem laços de feedback entre as partes componentes do sistema e entre estes componentes e as estruturas que emergem em níveis hierárquicos mais altos.
Grande Número de Componentes Independentes: Uma vez que a origem da auto-organização recai nas conexões, interações e laços de feedback entre as partes dos sistemas, torna-se claro que sistemas auto-organizáveis devem possuir um grande número de componentes.
Comportamento geral independente da estrutura interna dos componentes: Isto quer dizer que não importa do que ou como são feitos os componentes do sistema, desde que eles façam as mesmas coisas. Em outras palavras, isto significa, que a mesma propriedade emergente irá surgir em sistemas completamente diferentes.
Emergência: A emergência é provavelmente a noção menos conhecida dentre as que se relacionam com auto-organização [CRU94]. A Teoria da Emergência diz que o todo é maior do que a soma das partes e o todo exibe padrões e estruturas que surgem espontaneamente do comportamento das partes..
Comportamento geral organizado e bem definido: Desconsiderando a estrutura interna de um sistema complexo e observando-o apenas como um fenômeno emergente constata-se que seu comportamento é bastante preciso e regular.
Efeitos em Múltiplas Escalas: A emergência também aponta para interações e efeitos entre múltiplas escalas nos sistemas auto-organizáveis. As interações em pequena escala produzem as estruturas em grande escala as quais por sua vez modificam a atividade na pequena escala.
Uma estrutura de feedback é um laço causal, uma cadeia de causas e efeitos que forma um anel. Dentre essas estruturas, a mais simples é o feedback de reforço, também conhecido como efeito bola-de-neve ou ciclo vicioso. A principal característica do feedback de reforço é ser auto-amplificador. Quanto mais complexo um sistema (seres vivos, por exemplo) maior o número de estruturas de feedback que apresenta. Tem sido observado que sistemas que apresentam feedback tendem a desenvolver propriedades completamente novas. Este fenômeno, como já se viu, denomina-se emergência e as novas propriedades do sistema são ditas propriedades emergentes.
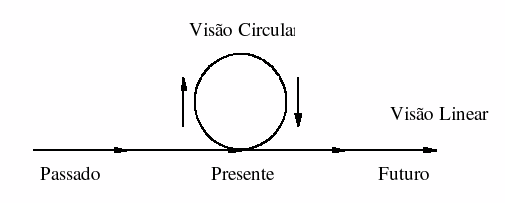
A metáfora da bola que rola e cresce ao mesmo tempo em que aumenta a velocidade ladeira abaixo além de representar muito bem o fenômeno demonstra também dois modos completamente diferentes de perceber o processo. A bola de neve apresenta dois movimentos diferentes: quando se acompanha a bola com os olhos, verifica-se que ela possui um movimento circular de rotação sobre si própria. Por outro lado, quando se observa a bola rolando ladeira abaixo vê-se que sua trajetória descreve uma linha reta. Os dois movimentos correspondem a duas formas fundamentalmente diversas de perceber o tempo.
Na tradição científica ocidental adota-se em geral a visão linear. O tempo é visto como passado, presente e futuro dispostos sobre uma linha. O presente é um ponto sobre esta linha, movendo-se em direção ao futuro e deixando o traço do passado atrás de si. Na visão linear as causas estão sempre atrás dos efeitos. Isto entretanto não é o caso na visão circular, onde causa e efeito estão conectados em um ciclo. Não faz sentido falar em “na frente de” ou “atrás” em uma trajetória circular onde qualquer ponto está ao mesmo tempo na frente e atrás de outro ponto. A verdade é que cada uma dessas visões necessita da outra, pois correspondem a duas diferentes perspectivas de um mesmo fenômeno. A metáfora da bola de neve mostra claramente como estas duas perspectivas podem ser combinadas: um feedback é uma estrutura circular rolando sobre um tempo linear.

Figura 1
Duas visões complementares para estruturas de feedback
A onda é um padrão muito comum, considerado por alguns como emergente. Um dos exemplos que melhor descrevem uma onda é o efeito dominó. Causa grande impressão observar dominós cairem sucessivamente, derrubados pela queda de seus antecessores, produzindo assim uma onda. Entretanto, se este é um padrão emergente, deve haver um ciclo em algum lugar. Observando cuidadosamente o efeito dominó pode-se considerar o mesmo comparável ao efeito produzido por uma esfera invisível, rolando sobre os dominós e derrubando-os em seqüência. Visto desta maneira, o efeito dominó lembra em muito o efeito bola de neve anteriormente citado. A esfera invisível possui o mesmo movimento e, como a bola de neve, deixa um rastro: os dominós tombados atrás de si. A visão circular do fenômeno é vista na Figura 2. Apesar das grandes diferenças, o efeito bola de neve e o efeito dominó compartilham a mesma estrutura subjacente e resultam portanto bastante similares. Esta similaridade, entretanto, permanece invisível a menos que se adote também a visão circular do fenômeno. No caso do efeito dominó, a representação adotada pode parecer estranha, tomando o efeito (a onda) pela causa imaterial (a esfera invisível), no entanto não se deve esquecer que ambos representam apenas diferentes visões de uma mesma estrutura de feedback.

Figura 2
Visão circular do efeito dominó
Freqüentemente comportamentos muito organizados surgem em sistemas de extrema complexidade. Exemplos óbvios disto são os organismos vivos. Bilhões de células interagem apresentando um comportamento notavelmente organizado. Ainda que os diversos fenômenos emergentes que ali ocorrem sejam muito diferentes uns dos outros, eles possuem algo em comum. Um conceito muito importante que conecta todos os fenômenos emergentes é o meta-balanceamento. Este é um conceito considerado chave para o entendimento da emergência. Um sistema meta-balanceado é um sistema que pode ser visto de duas diferentes perspectivas. A nível de detalhe o sistema está completamente desbalanceado, entretanto, de uma perspectiva global, o sistema parece ser estável e ordenado. O curioso aqui é que o sistema precisa estar desbalanceado internamente para produzir ordem global.
Este é talvez um dos aspectos menos intuitivos da teoria dos sistemas. Corresponde a afirmar que a maneira de produzir estabilidade emergente em um sistema é conduzi-lo internamente a um estado desbalanceado. O conceito entretanto é fácil de demonstrar. Tanto o efeito bola de neve quanto o efeito dominó são fenômenos meta-estáveis. No efeito dominó, por exemplo, há um comportamento claramente estável e ordenado no sistema - a onda. Mesmo assim o comportamento observado individualmente em cada dominó é de desequilíbrio. A esfera invisível é formada pelos dominós que caem e rola exatamente no ponto em que estes tombam, desbalanceados.
Um sistema dito balanceado ou em balanço é um sistema que não dispende energia. Consequentemente um sistema está desbalanceado quando dispende energia. Assim, para provocar o surgimento de fenômenos emergentes nos sistemas é necessário fazê-los dispender energia. Além disso deve-se continuamente alimentá-los com novos componentes e energia para sustentar o meta-balanceamento. Assim o efeito dominó somente pode ser mantido enquanto houver um novo dominó em pé na frente do que está caindo. Em outras palavras, é necessário alimentar-se constantemente a esfera invisível com novos dominós para mantê-la desbalanceada. Da mesma forma como a bola de neve precisa ser alimentada com mais neve para manter-se crescendo. Deste modo, ao contrário dos sistemas estáveis, sistemas meta-estáveis consomem muita energia. Em resumo, o conceito de meta-balanceamento é uma propriedade universal de todos os fenômenos emergentes.
Quando se observa a onda de dominós (ou uma onda no oceano ou qualquer outra onda) tem-se a sensação que ela de algum modo sobrevive de um momento para o seguinte, isto é, a onda se apresenta como sendo única e de duração prolongada no tempo. A questão é que quando a onda se auto-reproduz, avançando para o momento seguinte, ela o faz a partir de componentes diferentes. Assim, se a onda emergente for observada da perspectiva dos dominós ela não será a mesma onda. Isto é verdadeiro para todos os fenômenos emergentes.
Na esfera dos seres humanos tem-se a sensação de sobreviver de um instante para outro, no entanto o que realmente ocorre é um contínuo processo de substituição de componentes. Nova energia e novas moléculas fluem continuamente no organismo humano, onde o ciclo de substituição ao nível molecular dura cerca de sete anos. Este é o período em que todas as moléculas do corpo humano são substituídas por novas. No efeito dominó o ciclo dura apenas uma fração de segundo. Assim, quando se fala em sobrevivência e uniformidade deseja-se referir a estrutura do sistema. Ainda que todos os componentes do sistema serem substituídos por novos, sua estrutura permanece fundamentalmente a mesma. Ficam assim evidentes as razões pelas quais os conceitos discutidos acima precisam ser considerados em conjunto, conforme a Tabela 1.
Tabela 1
Conceitos complementares segundo diferentes visões
|
Visão Circular |
Visão Linear |
|
Estrutura Perspectiva Global Meta-balanceamento Esfera Invisível |
Padrão Perspectiva do Componente Desbalanceamento Onda |
A teoria da complexidade se relaciona muito de perto com a teoria dos sistemas. Ambas por sua vez estão relacionadas com a teoria do caos e com a cibernética. A grosso modo esse relacionamento pode ser resumido como se apresenta na Tabela 2
Tabela 2
Objetos de diferentes teorias
|
|
Sistemas |
Comportamento |
|
Teoria dos Sistemas |
simples |
simples |
|
Teoria da Complexidade |
complexos |
simples |
|
Teoria do Caos |
simples |
complexo |
|
Cibernética |
complexos |
complexo |
A teoria dos sistemas e a teoria da complexidade se sobrepõem e são baseadas nos mesmos princípios. Qual seria então a necessidade de duas disciplinas distintas? A razão principal parece ser o fato de que ambas pertencem a duas diferentes tradições científicas, entretanto há certamente outros motivos. Nem todos os sistemas são tão simples como a galinha e o ovo. Em um sistema constituído por milhões de componentes seria quase impossível projetar uma estrutura circular descrevendo todos os possíveis laços de feedback. Somente é possível esquematizar o feedback de uma forma muito geral, como é mostrado na Figura 3.
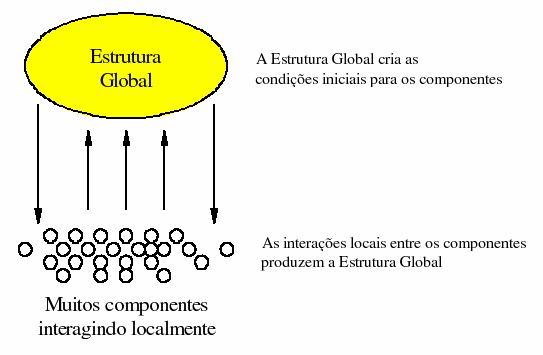
Figura 3
Feedback em sistemas complexos
Como o diagrama sugere, há um relacionamento circular entre a estrutura global do sistema e as interações locais entre os componentes. A estrutura global pode ser definida como a rede de todos os relacionamentos locais, que é produzida e mantida em um dado momento pelo total de interações que ocorrem neste momento. Cada um e todos os componentes do sistema interagem com seus vizinhos imediatos, modificando assim a estrutura global. Uma vez que cada componente responde à estrutura global, então o comportamento de cada indivíduo é determinado pelo todo. Ao mesmo tempo a resposta independente de todos os componentes em um dado momento produz o todo do momento seguinte. Um exemplo de sistema complexo é uma sociedade. Uma sociedade consiste em muitos componentes independentes interagindo localmente. O estado corrente da sociedade é a estrutura global. Cada um e todos os indivíduos respondem ao estado corrente e portanto criam o novo estado da sociedade no momento seguinte e assim por diante. Assim um sistema complexo pode ser definido como sendo constituído por muitos componentes independentes que interagem localmente produzindo um comportamento geral organizado e bem definido independente da estrutura interna dos componentes.
Redemoinhos em águas revoltas e tornados em céus turbulentos são exemplos perfeitos de vórtices. O curioso sobre os vórtices é que parece haver alguma força em seus centros sugando grandes massas a partir de um ponto impreciso. Isto entretanto é apenas uma ilusão ocasionada pelo movimento das massas em círculo. Se estas forem removidas do vórtice não resta absolutamente nada. É como remover as cascas de uma cebola esperando encontrar algo em seu interior. Entretanto, observando-se os vórtices, fica claro que existe uma força em algum lugar. Onde está ela? A resposta é talvez uma das mais importantes noções da ciência da complexidade: ela vem de dentro do sistema. Ainda que na aparência uma força externa esteja organizando o vórtice, são as próprias massas em movimento circular que animam o fenômeno. Uma das razões pela qual este conhecimento é tão importante é que ele encerrou a longa disputa entre o vitalismo e o materialismo. Os vitalistas defendiam a idéia de que a existência da vida depende de uma força vital, enquanto que os materialistas acreditavam não ser necessária nenhuma força externa para produzir vida. O estudo dos vórtices mostra que ambas as visões estão corretas. Os vitalistas, bastante acertadamente, identificaram uma força vital, que corresponde à força de sucção ilusória existente no centro do vórtice. A visão materialista é também correta, uma vez que tal força vital emerge do interior do sistema. Nada do exterior está organizando o vórtice. A força vital é real, mas não existe no sentido usual de existência, possuindo o que se denomina uma hiper-existência. Para que ocorra a hiper-existência é necessário satisfazer as seguintes condições:
O fenômeno emergente deve estar incorporado,
Os componentes do sistema devem estar desbalanceados, e
Deve haver feedback no sistema.
Todas essas três condições são satisfeitas pelos vórtices: (1) Um vórtice não pode emergir no vácuo, ele necessita estar incorporado em um meio físico. Isto corresponde à primeira parte da definição de um sistema complexo: um sistema complexo consiste em muitos componentes independentes. (2) Um vórtice não pode emergir a menos que as massas de ar ou água que o compõem estejam em movimento (desbalanceadas). Finalmente, (3) um vórtice é por si próprio uma estrutura circular, possiblilitando a ocorrência de feedback. Quando essas três condições são satisfeitas, a força ilusória de sucção emerge no centro do vórtice.
Além do efeito bola-de-neve, do efeito dominó e do vórtice, há um quarto fenômeno emergente que deve ser observado: a ressonância. Como se verá a seguir a ressonância possui exatamente as mesmas propriedades das três outras estruturas. Além disso, enfatiza outras importantes propriedades dos sistemas complexos. No sentido usual com que a palavra é empregada, ressonância é um som prolongado por um processo repetitivo. Pode ser produzida pelo uivo do vento, por um apito, por uma guitarra elétrica ou um órgão tubular. A definição técnica de ressonância é basicamente a mesma, exceto que não está restrita a ondas sonoras, generalizando a idéia para qualquer tipo de onda. O que se denominou processo repetitivo é exatamente algum tipo de feedback. Na Figura 4 apresenta-se um tipo de ressonância sonora que é um problema comum entre os músicos.
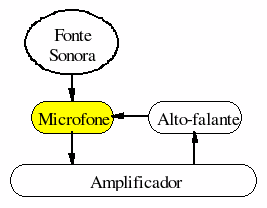
Figura 4
Ressonância sonora
O som captado pelo microfone é amplificado e retorna ao ambiente através do alto-falante. Daí este som amplificado passa a ser também captado pelo microfone e a bola de neve começa a rolar novamente. O resultado audível é um som muito agudo e alto que pode inclusive danificar equipamentos mais sensíveis. Uma análise do espectro deste som mostra a evolução emergente de um pico senoidal, que cresce e se torna cada vez mais alto, terminando em uma única freqüência, como é mostrado na Figura 5. Este é o padrão característico de desenvolvimento de uma onda de ressonância A novidade aqui é a redução de informação: o som original, composto de muitas freqüências, termina em uma única freqüência.
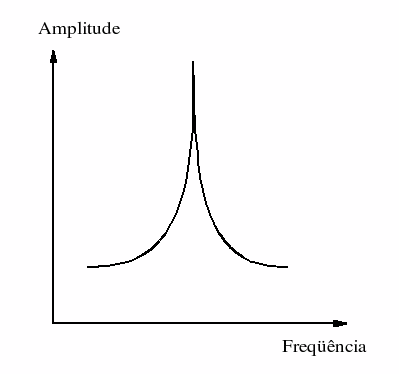
Figura 5
Ressonância como um redutor de informação
Em outras palavras, a ressonância age como um filtro emergente. Sua estrutura de feedback filtra todas as freqüências deixando apenas uma. Mas, além de filtrar todas as outras freqüências, ela amplifica a freqüência restante. Por esta razão a ressonância é considerada um filtro ativo na teoria dos filtros. Deve-se notar aqui a similaridade entre o vórtice e a ressonância. No vórtice há uma força ativa no centro que suga a matéria em sua direção. Na ressonância um sistema de freqüências é sugado e aprisionado em um único padrão.
Viu-se então que as estruturas de feedback podem atuar como filtros emergentes, caracterizando processos de redução de informação. Este processo pode ser entendido como uma forma de seleção. Há cerca de 150 anos atrás, o grande biólogo Charles Darwin descobriu que o mecanismo de evolução biológica correspondia exatamente a um processo de seleção, que ele denominou seleção natural, e que este processo nada mais era do que a sobrevivência do melhor adaptado. Os organismos que não se adaptaram ao longo da cadeia evolutiva foram extintos, isto é, filtrados para fora do processo. Darwin viu os organismos como se fossem máquinas perpétuas, atravessando um processo de filtragem natural. Somente as verdadeiramente perpétuas conseguiam atravessar o filtro. O significado de uma máquina perpétua no contexto da complexidade é o de mecanismos capazes de perpetuar sua execução e de se reproduzir. Os organismos vivos caem exatamente na categoria das máquinas perpétuas.
Os organismos agem como se imbuídos da seguinte missão: manter-se em funcionamento por tempo suficiente para produzir cópias de si próprios. Para manter-se em funcionamento necessitam de um contínuo fluxo de energia e matéria através de si próprios. Em outras palavras, necessitam comer. Em comparação se poderia dizer que um carro mantém-se em movimento comendo gasolina. Isto não significa, evidentemente, que o carro esteja vivo. O problema é que o carro não faz nenhum esforço de moto próprio para obter mais gasolina. Os organismos deveriam ao menos usar a energia proveniente de seu alimento para obter mais alimento e então reproduzir-se. Analogamente, na seleção natural, os que não forem capazes de obter alimento e reproduzir-se (isto é, os inadequados) serão retidos pelo filtro.
A seleção natural não é somente um filtro, ela é também uma ressonância que amplifica os organismos adequados enquanto que os inadequados vão sendo retirados de cena. Entretanto, para ser realmente criativa a seleção natural precisa estar desbalanceada. Como desbalancear um sistema biológico? A resposta é: levar os organismos a competir por recursos limitados. Quando os organismos competem eles tornam a própria adequação instável. O que hoje é adequado pode não o ser amanhã. Um cenário de adequação dinâmica é fonte de novos fenômenos emergentes que tornam a seleção natural mais do que um mero processo de filtragem passiva. A adequação dinâmica produz criatividade e inteligência. Este é o fenômeno emergente mais importante de todos, porque abre o caminho para a evolução da evolução. Isto pode ser constatado na seleção natural, na evolução da mente e na evolução cultural dos povos.
Sistemas complexos são todos constituídos de outros todos. Um relógio, por exemplo, não é um sistema complexo por ser constituído de partes e não de todos. A remoção de uma mola traz conseqüências fatais para o relógio, que simplesmente deixa de funcionar. Um sistema complexo, por outro lado, não é criticamente dependente de seus componentes, que por sua vez são outros todos. Se uma célula morre ou uma formiga se perde isto tem pouco efeito sobre o sistema ao qual pertencem. Para estar em meta-balanceamento um sistema complexo precisa estar desbalanceado ao nível dos componentes. Como colocar sistemas complexos em desbalanceamento? Simplesmente dando independência e liberdade a seus componentes. Sistemas complexos são meta-estáveis porque são constituídos de todos independentes que interagem. Quanto mais liberdade possuem os componentes, mais desbalanceado se torna o sistema e isto é fonte de mais meta-estabilidade global. Tudo isto traz claras evidências de que a natureza de alguma forma oscila entre o caos e a ordem.
Sistemas auto-organizáveis apresentam freqüentemente uma forma altamente complexa de organização. As colmeias, por exemplo, tem padrões óbvios e regularidades mas não são estruturas simples. Elementos estocásticos afetam a estrutura e a dinâmica de uma colmeia obtendo respostas variáveis e não determinísticas. Da mesma forma as nuvens, padrões climáticos, correntes nos oceanos, assembléias comunitárias, economias e sociedades, todos exibem formas complexas de auto-organização.
Não há uma definição geral apropriada para complexidade, apesar desta ser considerada de muitas formas. Intuitivamente a complexidade encontra-se em algum lugar entre a ordem e o caos, entre a superfície espelhada de um lago e a turbulência de um maremoto. A complexidade tem sido medida através de entropia métrica, profundidade lógica, conteúdo de informação e outras técnicas semelhantes. Estas medidas são adequadas a aplicações específicas da química e da física mas nenhuma delas descreve completamente as características da auto-organização.
Uma forma de abordar o estudo da complexidade, considerando a ausência de uma definição satisfatória, é descrever um certo espaço, compreendido entre a ordem e o caos, denominado a fronteira do caos [PAC88, LAN90, KAU91, KAU93]. Em 1990 Chris Langton [LAN90] conduziu um experimento empregando autômatos celulares (AC), onde tentava descobrir sob que condições um AC simples poderia suportar primitivas computacionais, tais como transmissão, armazenamento e modificação de informações. Em seu experimento um AC unidimensional é composto por 128 células conectadas em círculo. Cada célula apresenta quatro possíveis estados internos e recebe todos os seu inputs das demais células em sua região, denominada sua vizinhança. A vizinhança definida por Langton era constituída por cinco células. Cada célula é considerada membro de sua própria vizinhança, juntamente com suas duas células vizinhas de cada lado. O estado interno das células no momento seguinte é determinado pelo estado de sua vizinhança e alguma função de transição que descreve qual o novo estado que a célula deve assumir para um dado estado de sua vizinhança. Assim o estado da vizinhança é associado com a transmissão, o estado interno do autômato com o armazenamento e a função de transição com a modificação da informação.
Para determinar como a ordem e o caos afetavam a computação, Langton formulou um valor lambda que descrevia a probabilidade de uma dada vizinhança produzir em uma célula um determinado estado interno particular, denominado estado quiescente. Quando lambda assumia o valor zero, todas as vizinhanças moviam uma célula para o estado quiescente e o sistema era imediatamente organizado. Por outro lado, quando lambda assumia o valor 1 nenhuma vizinhança se movia para o estado quiescente e o sistema mantinha-se desordenado.
O experimento de Langton mostrou a existência de um valor crítico para lambda, correspondendo a pontos de transição de fase, em cuja proximidade a organização computada pelo sistema é máxima. Por outro lado, caso esse valor fosse ultrapassado, o caos surgia muito rapidamente. Segundo Langton, devido a associação da computação com tal valor crítico, um sistema auto-organizado precisaria manter-se na fronteira do caos para conseguir computar a própria organização.
As transições de fase nem sempre ocorrem de forma brusca como quebra entre dois estágios. Por exemplo, a passagem de um líquido do ponto de congelamento para o de ebulição se dá de forma gradual entre um estado e outro. Entretanto, a transformação do estado líquido para o gasoso nas vizinhanças de temperatura de ebulição se dá num espaço muito estreito entre os dois estados. Após um aquecimento gradual ocorre uma mudança brusca para o estado de gás, de forma que as duas fases são claramente distintas, separadas por uma estreita região que apresenta as condições de transição de fase. O estudo de tais regiões é normalmente muito útil para a previsão das propriedades do sistema ou substância em diferentes condições.
Em um estudo pioneiro, Per Bak e seus colaboradores. [BAK88] investigaram o comportamento de sistemas dinâmicos espacialmente estendidos empregando simulações em computadores de um modelo que haviam desenvolvido e denominado “monte de areia”. Neste modelo grãos de areia vão sendo continuamente depositados sobre uma mesa. Em um certos momentos o monte está tão alto quanto possível para sua base e então a areia escorrega pela encosta aumentando a base e permitindo ao monte continuar crescendo. O monte de areia é muito sensível a perturbações (se a mesa for sacudida mais areia cai pelas encostas) mas os valores obtidos para a inclinação máxima do monte de areia, apesar de não se apresentarem absolutamente regulares, flutuam dependendo das condições iniciais e da perturbação exercida sobre o sistema. Devido a este equilíbrio estável, ainda que precário, Bak e sua equipe concluíram que o sistema se apresentava em estado crítico. Além disso notaram que o sistema se auto-organizava em direção ao estado crítico sem necessidade de nenhum ajuste ou sintonia: quaisquer que fossem as condições iniciais o sistema tendia sempre ao estado crítico. Este fenômeno recebeu a denominação de criticalidade auto-organizada. Especula-se que este conceito possa ser fundamental para a escalabilidade espacial e temporal em sistemas dissipativos em desequilíbrio.
Sole e Manrubia [SOL95] usaram a teoria de Bak para examinar se o desenvolvimento de florestas exibia criticalidade auto-organizada. Sabendo que a queda de árvores e formação de clareiras é vital para a dinâmica das florestas tropicais eles propuseram que a distribuição e abundância de clareiras seria um indicativo do estado organizacional da floresta. Testando esta hipótese eles propuseram que as clareiras da floresta existente na ilha de Barro Colorado iriam apresentar uma distribuição auto-similar em multiescala. Esta hipótese foi sustentada tanto por dados empíricos quanto por simulações em computadores denominadas o jogo da floresta. Além disso as florestas simuladas também apresentaram propriedades fractais. Uma abordagem semelhante foi empregada no estudo de colônias de formigas do gênero leptothorax onde se verificou que a existência de uma densidade crítica de indivíduos que possibilita a informação máxima da colônia. Quando esta densidade é atingida, a colônia desenvolve pulsos de atividade que exibem auto-similaridade.
Em sistemas bióticos, um elemento importante na lista de mecanismos e condições que caracterizam a auto-organização é a habilidade que os agentes apresentam de se adaptar ao meio em que se encontram. Isto significa que os agentes são capazes de alterar suas funções internas de processamento de informações. Sistemas que apresentam tal característica são denominados sistemas complexos adaptativos (SCA) [HOR95]. No modelo de Langton as células seriam capazes de sintonizar suas regras de transição (e conseqüentemente seus valores lambda) ao longo do espectro entre o caos e a ordem. Em colônias de formigas leptothorax isto significa que as formigas que inicialmente não respondiam à modificações na densidade da colônia, ou o faziam de maneira adversa, acabariam por adaptar suas respostas de modo a conduzir à criticalidade auto-organizada. Ao se considerar a adaptação, uma série de novas questões sobre sistemas auto-organizados surgem: Quais são os mecanismos da adaptação? Sob que condições eles são possíveis? Este movimento se dá sempre na direção da criticalidade auto-organizada?
Em termos evolutivos a criticalidade auto-organizada seria obtida através das condições para a evolução (variação fenotípica individual, reprodução em excesso e herança de características genéticas). Uma população seria capaz de adaptar-se através da herança de variações genéticas introduzidas por mutação e recombinação. A causa da criticalidade auto-organizada seria a seleção natural. Uma população poderia evoluir na direção de um estado crítico porque a seleção natural removeria as variantes do sistema que se afastassem do estado crítico.
Stuart Kauffman [KAU91, KAU93, KAU95] desenvolveu uma rede booleana para a modelagem de SCA. Em seu modelo N unidades, cada uma das quais capaz de assumir A estados e conectada a K outros agentes são mapeadas em um panorama K-dimensional que expressa topograficamente todos os estados possíveis do sistema. Kauffman associou valores de adequação a cada um dos A estados assumidos por uma unidade de modo que quando os estados do sistema eram calculados através das K conexões entre N agentes, apareciam picos de adequação no panorama, representando estados ótimos do sistema. No modelo de Kauffman é possível obter panoramas em um sistema adaptativo para representar agentes, genomas, populações, etc. Sobrepondo diversos destes panoramas para estudar a co-evolução, Kauffman descobriu que K é um dos principais determinantes do grau de organização dinâmica de um sistema complexo.
Apesar de exigir ainda um grande esforço de pesquisa na construção de uma teoria unificada, o conceito de auto-organização apresenta excelentes perspectivas de aplicação em simulação, modelagem científica e otimização [DEC97].. Mecanismos encontrados em sistemas auto-organizáveis tem sido identificados com possíveis fontes de auto-organização em diversas áreas da física, química, biologia, economia, sociologia, comunicação, informação, educação, etc. [BRO94, HIE94].
Diversos tipos de modelos baseados em indivíduos foram desenvolvidos e pesquisados, incluindo redes de autômatos celulares (AC) [CAS91, LAN94], sistemas de vida artificial (A-Life) [KAW94] e modelos de clareiras em florestas [SHU92]. O interesse em tais modelos reside na possibilidade de aplicar suas propriedades estatísticas em modelos análogos do mundo real.
O principal atrativo da Internet é a facilidade que oferece à distribuição e comunicação de idéias e conhecimento. Sua estrutura, baseada no princípio da descentralização de operações e controle, possibilita uma interação muito mais direta entre produtores e consumidores de informações do que ocorre por exemplo na área de publicações, na televisão ou na indústria cinematográfica. A World Wide Web (WWW ou simplesmente Web) é o serviço da Internet que maior crescimento apresentou nos últimos anos. Seu maior apelo é oferecer aos seus usuários um interface agradável e relativamente eficiente para o acesso ao conhecimento desejado. Isto é obtido com o uso do protocolo HTTP (Hyper Text Transfer Protocol), que permite integrar a informação e seu interface com o usuário em uma única representação.
A WWW adota o princípio da distribuição na representação de conhecimento, o que significa que este é armazenado como uma rede de nodos e links. Os nodos podem conter qualquer combinação de texto, imagens, som, vídeo, etc. Os links conectam os itens individuais de um nodo para outro de acordo com a preferência de seus autores, formando algo assim uma rede de conceitos conectados através de relacionamentos informais. Os usuários navegam nesta rede perseguindo os links que lhes são significativos entre um nodo e outro. Neste processo empregam uma forma de julgamento associativo que visa conduzir a partir de uma certa posição inicial ao nodo ou nodos que contém a informação desejada.
Assim a organização material da WWW é produzida por seus projetistas que usam suas idéias intuitivas de estruturação do conhecimento e semântica na construção de nodos e sub-redes. Estas contribuições individuais são integradas gradualmente a corpos mais amplos de conhecimento preexistentes na WWW, assim expandindo o conhecimento da rede como um todo. Diversos elementos influenciam neste processo de organização de conhecimento, inclusive fatores psicológicos, lingüísticos, sociais e culturais, interesses e motivações dos autores e usuários das páginas WWW.
Esta organização uma vez materializada na rede assume uma representação dinâmica, objetiva e em geral de duração prolongada. Os novos nodos e links introduzidos modificam-se relativamente pouco ao longo do tempo. As modificações que ocorrem na rede são fruto de procedimentos de atualização, remoção e principalmente adição de conhecimento, sob a forma de nodos e links. Tais procedimentos produzem modificações concretas na rede e em geral são controlados pelos próprios produtores da informação. Eventuais inconsistências decorrentes de modificações materiais na rede, como links para nodos inexistentes ou nodos com features não suportadas por certos browsers, não possuem ainda uma solução satisfatória.
Por outro lado, o que se poderia denominar organização virtual da rede é produzida pelo processo dinâmico de navegação, o qual decorre da percepção semântica associativa dos usuários, ativando determinados links, que lhes parecem mais promissores ou interessantes em detrimento de outros que o são menos. No atual estágio tecnológico da WWW o conhecimento produzido pelo processo de navegação não é registrado sistematicamente, sendo portanto desperdiçado. No entanto - e este é o foco deste artigo - poderia ser empregado na construção de modelos auto-organizáveis de aprendizado associativo, em um sentido muito próximo ao proposto por Bollen em [BOL96], onde a WWW é vista como uma memória associativa de grandes dimensões.
Francis Heylighen [HEY96] propõe que o primeiro passo para tornar uma memória associativa mais eficiente é permitir que ela própria descubra a melhor organização possível para si própria. Na mente humana, conhecimento e significado se desenvolvem mediante um processo de aprendizado associativo: os conceitos que são mais freqüentemente usados juntos se tornam mais fortemente conectados. É possível implementar mecanismos similares na WWW criando associações com base nos caminhos percorridos pelos usuários através da rede de links. O princípio é simplesmente este: os caminhos percorridos por mais usuários se tornam mais fortes, enquanto que links raramente usados se tornam mais fracos.
Uma heurística simples pode então propor possíveis candidatos para novos links: Se um usuário navega de A para B e de B para C, é provável que exista não somente uma relação entre A e B mas também entre A e C (transitividade) e entre B e A (simetria). Desta forma novos links potenciais seriam continuamente gerados (variedade) mas somente aqueles que obtivessem determinada força seriam retidos e tornados visíveis ao usuário (restrição), enquanto que aqueles que não atingissem tal limiar de visibilidade seriam mantidos ocultos. Um experimento realizado sobre um sistema hipertexto adaptativo [BOL96] comprovou a exeqüibilidade desta idéia.
Uma das principais vantagens deste modelo de aprendizado associativo reside no fato de que ele funciona localmente (é necessário armazenar informações sobre nodos que estão no máximo dois passos adiante), mas a auto-organização que ele produz é global. Com tempo suficiente, nodos que se encontrassem a um número arbitrário de passos de distância poderiam se tornar diretamente conectados caso um número suficiente de usuários percorrer o caminho entre eles. O resultado esperado deste processo de aprendizado associativo é que os nodos que mais provavelmente serão utilizados em conjunto estarão também situados mais próximos na topologia da WWW.
Se tais algoritmos de aprendizado pudessem ser generalizados na WWW como um todo, o conhecimento ali existente poderia estruturar-se em uma rede associativa em permanente aprendizado. Cada vez que um novo nodo fosse introduzido seus links iniciariam imediatamente a adaptar-se ao padrão de seu uso e novos links não previstos pelo autor poderiam nele surgir se o seu potencial ultrapassasse um determinado limiar. Uma vez que tal mecanismo de certa forma assimilaria o conhecimento coletivo de todos os usuários da WWW, supõe-se que os resultados obtidos viriam a ser muito mais úteis, abrangentes e confiáveis do que qualquer sistema de indexação concebido segundo os interesses de indivíduos ou grupos. A mesma idéia também se aplica a contextos onde a organização da rede se daria a partir de um determinado ponto de partida - um servidor ou uma rede de servidores em uma organização - espalhando-se sem limites por toda a Web. A rede formada segundo tal principio certamente se aproximaria muito da semântica informal do grupo de usuários considerado, que poderia ser caracterizado sob muitos aspectos a partir desta representação.
O estudo das redes produzidas por auto-organização decorrente da observação da atividade de navegação na WWW pode levar ainda à identificação de estruturas e construções semânticas básicas, capazes de serem recombinadas na formação de representações mais complexas com múltiplas finalidades, tais como a otimização de redes de informações, mapeamento e representação do conhecimento compartilhado por especialistas, o provimento de um padrão para a identificação de idéias, etc.
[BAK88] Bak, P.; C. Tang; e K. Wiesenfeld: Self-organized criticality. Physical Review A 38:364-374, 1988.
[BOL96] Bollen, J.; Heylighen, F.: Algorithms for the Self-Organization of Distributed Multi-user Networks. In: R. Trappl (ed.). Cybernetics and Systems ‘96.. World Science, Singapore, 1996.
[BRO94] Brown, J. H.: Complex ecological systems. Pages 419- 443 in G. Cowan, D. Pines, and D. Meltzer (eds.) Complexity: metaphors, models, and reality. Addison-Wesley, Massachusetts, 1994.
[CAS91] Caswell, H.; J. E. Cohen. Communities in patchy environments: a model of disturbance, competition, and heterogeneity. p. 97-122 in J. Kolasa and S. T. A. Pickett (eds.): Ecological Heterogeneity. Springer, New York, 1991.
[CHA75] Chaitin, G.J.: A Theory of Program Size Formally Equivalent to Information Theory. Journal of ACM 13(1966) ibid 22(1975), .p.329.
[CRU94] Crutchfield, J. P.: Is anything ever new? In G. Cowan, D. Pines, and D. Melsner (eds.): SFI studies in the sciences of complexity XIX. Addison-Wesley, Massachusetts, 1994.
[DEC97] Decker, N.: Self-Organizing Systems. University of New Mexico. Biology 576: Landscape Ecology & Macroscopic Dynamics. Albuquerque, 1997.
[FOR94] Forrest, S.; T. Jones. Modeling complex adaptive systems with echo. P. 3-21 in R. J. Stoner and X. H. Yu, (eds.) Complex Systems: mechanisms of adaptation. IOS Press, Amsterdam, 1994.
[GEL94] Gell-Mann, M.: The Quark and the Jaguar. W. H. Freeman, New York, 1994.
[GRE93] Green, D. G.: Emergent behaviour in biological systems. P. 24-35 in D. G. Green and T. J. Bossomaier, editors. Complex Systems - From Biology to Computation. IOS Press, Amsterdam, 1993.
[HEY88] Heylighen, F.: Building a Science of Complexity. 1988 Annual Conference of the Cybernetic Society. Londin, 1988.
[HEY96] Heylighen, F.; Bollen, J.: The World Wide Web as a Superbrain: From Methafor to Model. In: Cybernetics and Systems ’96. World Science, Singapore, 1996.
[HIE94] Hiebeler, D.: The swarm simulation system and individual-modeling based. In Decision Support 2001: advanced technology for natural resource management, 1994.
[HOR95] Horgan, J. From complexity to perplexity. Scientific American (June 1995):104-109.
[HOU88] Huston, M., D. DeAngelis, and W. Post. 1988.: New computer models unify ecological theory. Bioscience 38:682-691, 1988.
[ISO97] ISOC - Internet Society: Internet Growth Statistics. February 1997. ftp://ftp.isoc.org/isoc/History/90s_host.txt
[ITO93] Ito, K; Y. Gunji.: Self-organisation of living systems: towards criticality at the edge of chaos. BioSystems 33:17-24, 1993.
[KAU91] Kauffman, S. A. 1991.: Coevolution to the edge of chaos: coupled fitness landscapes, poised states, and coevolutionary avalanches. Journal of Theoretical Biology 149:467-505, 1991.
[KAU93] Kauffman, S. A.: Origins of Order: self- organization and selection in evolution. Oxford Univ. Press, New York, 1993.
[KAU95] Kauffman, S. A.: At Home in the Universe. Oxford University Press, New York, 1995.
[KAW94] Kawata, M., and Y. Toquenaga.: Artificial individuals and global patterns. Trends in Ecology and Evolution 9:417-421, 1994.
[KIL96] Killen, J.: Internet: Global Penetration 1996 and Forecast 2000. December 1996. http://www.killen.com/ipf.htm.
[KOL65] Kolmogorov, A. N.: Three Approaches to the Quantitative Definition od Information. Problems of Information Transmission v1 n.1 pp. 1-1, 1965.
[LAN90] Langton, C. G.: Computation at the edge of chaos: phase transitions and emergent computation. Physica D 42:12-37, 1990.
[LAN94] Langton, C. G., (ed.): Artificial Life III. Addison-Wesley, New York, 1994.
[MIT93] Mitchell, M., P. Hraber, and J. P. Crutchfield. 1993. Revisiting the edge of chaos: Evolving cellular automata to perform computations. Complex Systems 7:89-130, 1993
[NIC89] Nicolis, G., and I. Prigogine: Exploring complexity. W. H. Freeman, New York, 1989.
[OLS95] Olson, R. L., and R. A. Sequeira: An emergent computational approach to the study of ecosystem dynamics. Ecological Modelling 79:95-120, 1995.
[PAC88] Packard, N. H. 1988. Adaptation toward the edge of chaos. P. 293-301 in A. J. Mandell, J. A. S. Kelso, and M. F. Shlesinger (eds.) Dynamic Patterns in Complex Systems. World Scientific, Singapore, 1988.
[PAL96] Palazzo, L.: Aspectos da Modelagem de Sistemas de Informações Inteligentes. Exame de Qualificação em Profundidade. CPGCC da UFRGS, Programa de doutorado, agosto de 1996.
[PER95] Perry, D. A. 1995. Self-organizing systems across scales. Trends in Evolution and Ecology 10:241-244, 1995.
[PRI84] Prigogine, I.; Stengers, I.: Order Out Of Chaos. Bantam Books, New York, 1984.
[SHU92] Shugart, H. H., T. M. Smith, and W. M. Post: The potential for application of individual-based simulation models for assessing the effects of global change. Annual Review of Ecological Systems 23:15-38, 1992.
[SOL95] Sole, R. V.; S. C. Manrubia.: Are rainforests self-organized in a critical state? Journal of Theoretical Biology 173:31-40, 1995.
[SOL95a] Sole, R. V.; O. Miramontes.: Information at the edge of chaos in fluid neural networks. Physica D 80:171- 180, 1995.
[SWE89] Swenson, R.: Emergent attractors and the law of maximum entropy production: foundations to a theory of general evolution. Systems Research 6:187-197, 1989.
[WAL92] Waldrop, M.M. Complexity: the emerging science at the edge of order and chaos. Simon & Schuster, New York, 1992.
[YAT87]Yates, F. E.(ed.): Self-Organizing Systems: the emergence of order. Plenum Press, New York, 1987.
[ZAK96] Zakon, R. H.: Hobbes’ Internet Timeline v.2.5, July 1996. http://info.isoc.org/guest/zakon/Internet